В этом разделе речь пойдет о растеризации двумерных графических примитивов, таких как отрезки, окружности, эллипсы. Мы попробуем разобраться, в чем отличие идеальных математических объектов от реальных отрезков и окружностей, рисуемых на экране.
При этом рассматриваются реальные задачи отрисовки графики, поэтому предложенные алгоритмы должны работать с приемлемой скоростью и использовать различные оптимизации.

Далее, на базе рассмотренных методов, будут построенны алгоритмы заливки фигур.

Связность

Идеальная математическая линия представляет собой бесконечное количество точек, удовлетворяющих определенному уравнению, или задана другим образом. Реальный экран это всегда конечное количество точек. Изображение представляет из себя прямоугольную сетку, узлы которой имеет целочисленные координаты. Появляется законный вопрос: как определить связность линии на экране?

Традиционно вводятся два понятия связности.

4-связность: пикселы p1(x1, y1) и p2(x2, y2) называются соседними, если либо разность их координат по оси x, либо разность их координат по оси y равна 1 (либо исключающее):

|x2 – x1| + |y2 – y1| <= 1

8-связность: пикселы p1(x1, y1) и p2(x2, y2) называются соседними, если разность их координат по оси x и разность их координат по оси y не больше 1:

|x2 – x1| <= 1, |y2 – y1| <= 1



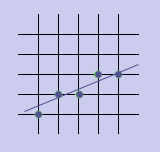
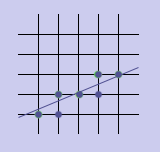
8-связность(рис 1.) и 4-связность (рис 2.)

Линией на растровой сетке будем считать последовательность пикселов {P1, …, Pn}, таких, что любые два пиксела Pi, Pi+1 являются соседними в смысле заданной связности.

Прим. Отметим, что любая четырехсвязная линия одновременно является восьмисвязной, но не наоборот. Таким образом 4-связность является более сильным понятием.

Отсечение

Понятие связности, введенное выше, позволяет обойти требование на целочисленность координат всех точек. С помощью этого понятия можно судить о связности дискретной линии. Другая проблема состоит в том, что область вывода всегда имеет ограниченные размеры. Область формы, на которую делался вывод в предыдущих разделах, имеет форму прямоугольника. Таким образом появляется задача отсечения выводимых геометрических примитивов по границе некоторой области. Алгоритмы отчесения будут рассмотрены ниже.

Переход к оконным координатам

В предыдущем разделе не акцентировалось внимание, где именно стоит перейти из логических координат в оконные. Дискретность сетки, на которую выводится изображение, имеет определенные преимущества. А именно, за счет целочисленности коорднат пикселей можно создать алгоритмы, которые будут также работать только с целыми числами. Более того, во многих случаях основной цикл из числа арифметических операций содержит только сложения!

Становится ясно, что переход к оконным коодинатам нужно осуществить до начала работы основного алгоритма. В общем случае схема работы будет выглядеть следующим образом:

Код

/*
В функцию передаются точки с логическими координатами.
*/
void DrawLine(_Point p1, _Point p2){
// преобразовываем в оконные координаты
p1 = viewport->T(p1);
p2 = viewport->T(p2);
// делаем отсечение
ClipLine(p1, p2);
// основной алгоритм
// ...
}

Это то, что касается базовых понятий. В последующих статьях будут рассмотрены математические основы задания графических примитивов и алгоритмы их построения (растеризации).